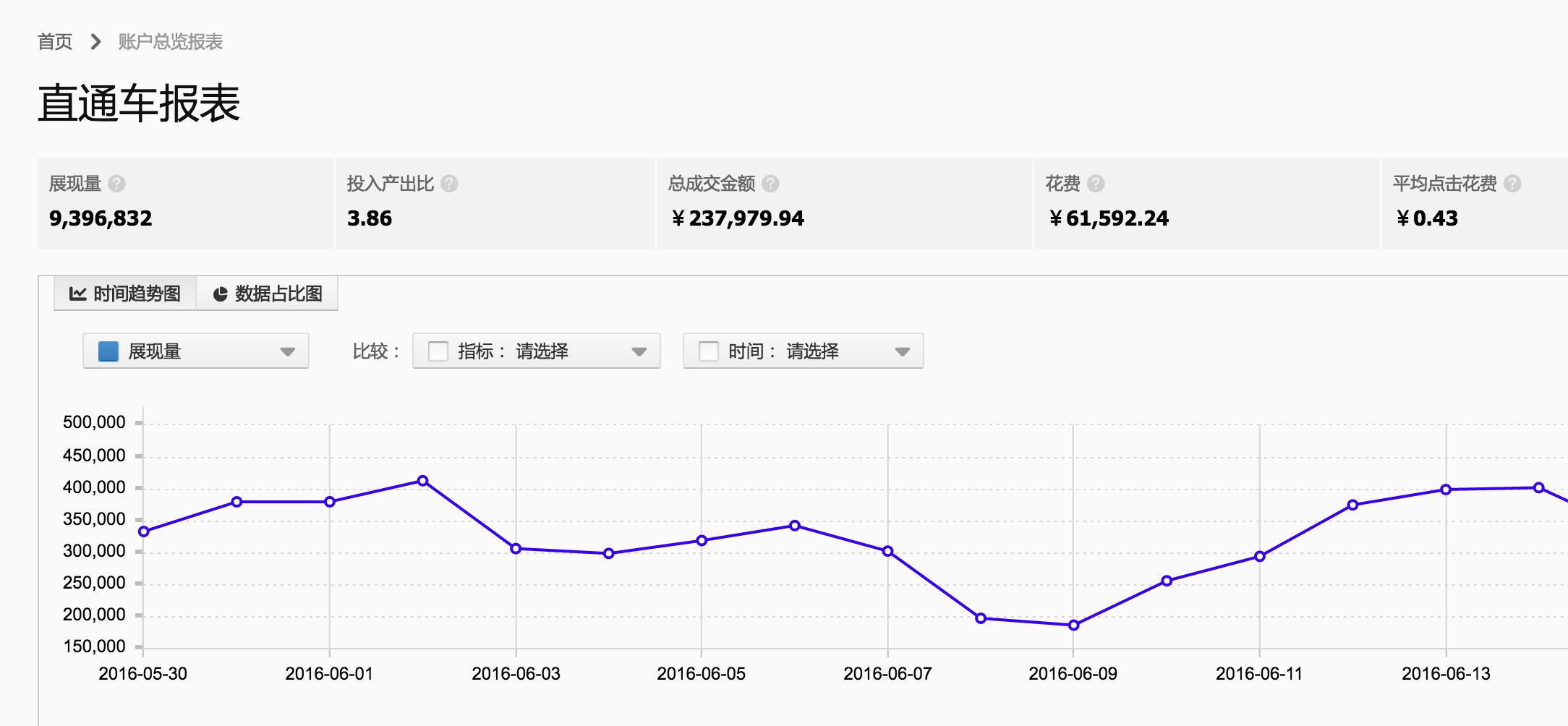
开车6载，直通车扣费公式已经深入我心，已经看之为真理，为公式，彷佛就该如此，但吾却从没想过，公式从哪里来，为什么公式是这样的，又是谁发明了这个公式
我们先来看直通车的扣费公式
你的扣费＝下一名的质量得分＊下一名的出价／你的质量得分＋0.01
搜索广告的竞价机制可以抽象为一种广告位拍卖机制。在搜索广告平台上，广告主会为自己的广告选择一些相关的关键字，并在这些关键字下出具不同的竞价。这样，对于一个给定的关键字，可以关联上若干条不同的广告，每条广告有不同的竞价，这些广告在广告系统中形成了一个竞拍关系，竞拍的目标是一次关键字命中后，系统中空出的若干条广告位。形式化而言，假设有A＝｛a1,a2,a3,…an｝，n个广告，另外广告平台提供S={s1,s2,s3…sn}，m个广告位，这里m<n。广告位拍卖的目的是从a中选取m条广告，依次放置到s中。如果广告ai被点击了，广告系统需要ai的广告主收取一定的费用。对于通常的广告系统，即使是同一次广告展现，不同的展现位置收到的用户关注度也会不同。例如，百度的搜索广告中，广告的展现形式是自上而下的排列若干条广告，这种展现形式中，排第一位的广告天然会有更高的点击率。因此，对于广告主而言，每次关键字拍卖竞争的不仅是是否获得展现机会，还包括在s中的排序位置。不难看出，广告位的拍卖过程大致可以分为两个步骤，广告排序和广告扣费。广告排序解决当关键字命中后，展现哪些广告的问题。广告扣费则关心当广告被点广告排序解决当关键字命中后，展现哪些广告的问题。广告扣费则关心当广告被点击后，向广告主收取多少费用的问题。互联网广告的不同发展时期，不同的公司，使用的广告排序方式和广告扣费方式有所不同。在后面的三节中，我们会讨论三种比较常见的排序方法和扣费机制。这里，我们先讨论一些拍卖理论中评价拍卖策略优劣的通用指标。
拍卖理论中，竞拍各方通过相互博弈，竞争待分配的资源，形成最终交易。在竞拍过程中，如果存在一点，博弈各方如果改变竞价策略就会导致利益损失。这一点，就被称为纳什均衡点。存在纳什均衡点，表示该拍卖策略存在一种稳定状态，在这个状态下，博弈双方如果做出策略改变，就会导致利益损失，因为各方都趋于保持该状态。在互联网关键字拍卖中，广告主可能会频繁的修改自己的出价。因此，关键字拍卖的博弈过程是一种无限重复的博弈，这种博弈过程会有很多不同的纳什均衡点。过多的均衡点不便于分析拍卖策略的效果，于是有人提出一种本地无嫉妒均衡（locally envy-free equilibria），又称对称纳什均衡。本地无嫉妒均衡是指，排在第k位的广告主，如果增大出价排到第k-1位，不会增加其收益。
与纳什均衡相关联的一个概念是占优策略，占优策略是指无论竞争对手采取什么策略，都能使本方获得最大利益的策略。与纳什均衡不同的是，占用策略不考虑其他竞争者的策略，都能保证自己利益最大。
此外，关键字拍卖希望广告主按照自己的真实估价出价，并通过调整扣费方式来激励用户按照真实估价出价。如果竞拍方按照真实估价出价，能够保证其获得最大利益，则该竞价策略称为激励相容。
广义一阶价格（GFP）
世界上首例互联网广告诞生于1994年，与现在主流的计费方式不同，早期的互联网广告大部分采取按照展现收费的方式。在那段互联网广告的原始时代，既没有自动投放系统，也没有自动计费系统。广告主通过线下签订商业合同的方式，从互联网媒体那里购买从一定流量。一般来说，每笔交易涉及的流量大约只有几千次展现。即便如此，广告的花费却比如今的广告贵很多，通常广告主一个月大约要花费几千美金。更糟糕的是，这种线下交易的方式，通常操作起来流程相当复杂，广告主往往需要等待很长时间才能看见自己的广告生效。
1997年，Overture公司（已被Yahoo!收购）提出了一套全新的广告售卖机制，就是所谓的竞价排名机制。广告主选择跟自己商品相关的关键字，并对它竞价。用户输入关键字时，搜索引擎按照竞价由高到低的顺序，自上而下的展现相关广告。这样展现的原因是，通常情况下，越靠上的广告位越能吸引用户的注意，因而商机越好。与早期的互联网广告不同，在Overture的商业模式中，广告展现并不扣费，只有当用户点击了某个广告，才会扣除广告主竞买这个关键字的价格。按照这样的商业模式，Overture开发的广告投放系统，在当年一炮走红，成为Yahoo!和MSN等知名搜索引擎的广告提供商。
Overture的拍卖策略就是所谓的广义一阶价格拍卖，这里的一阶价格是指广告主本身的出价。广告的排序方式采取按照竞价降序排列，然后选取排序较高的前几个广告用于展现。在广义一阶价格模式的扣费方法是，如果广告发生点击了，便会按照广告主的竞拍出价，进行扣费。
但是Overture的成功背后却隐藏着巨大的危机。因为理论上来说，广义一阶价格排序不存在纳什均衡点。所以当Overture支持快速改价功能后，于是市场上出现了竞价机器人，帮助广告主在不丢失自己想要广告位的情况下，不断尝试降低竞价。比如说，现在有三个广告位售卖，a、b和c三个广告主分别出价￥6，￥4和￥1。如果，b使用竞价机器不断调价，那么为了保住他第二名的广告位，竞价机器人最终只要给出￥1.01就可以了。同理，如果a也使用竞价机器人，那么a为了保住第一名的广告位，只要给出￥1.02即可。因此，竞价机器人的出现，导致广告系统的收益大大降低。此外，竞价机器人的频繁改价，也极大的加重的广告系统的负载。
广义二阶价格（GSP）
Google意识到，竞价机器人的出现实际是广义一阶价格模式激励了广告主不断调低竞价，以便降低自己的广告成本。于是，Google提出了自己的计费机制，该机制被称为广义二阶价格。对应第i位的广告，如果发生点击，那么广义二阶价格扣费是，收取第i位广告主，第i+1位广告竞价加上一个货币最小值。在上一段的例子中，广告主a和b发生点击的收费分别是￥4.01和￥1.01。在广义二阶价格中，广告主降低其竞价，在其展现位置不变的情况下，不会降低收费。因此，杜绝了竞价机器人对广告系统的恶劣影响。此外，因为下家没有降低竞价的行为，其结果导致上家需要付出更多的点击费用。如果人人皆如此，广告系统的实际收益反而会比广义一阶价格更多。
对于广义二阶价格，存在所谓本地无嫉妒均衡，举例说明
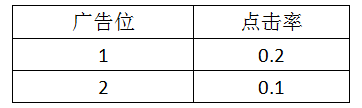广告位和点击率
广告和点击
设A、B、C三条广告竞争1、2两个广告位，其中1、2的点击率以及A、B、C的每次点击价值如上表。那么（4，1，0.5）是一个均衡报价。因为，任意一方如果加价是的排名升高，都会导致利益降低。
形式化的，对于
A＝｛a1,a2,a3,…an｝，n个广告，每条广告的点击价值为
V＝｛v1,v2,v3…vn｝，另外广告平台提供
S={s1,s2,s3…sn}，每个位置的点击率为
X={x1,x2,x3…xn}，每个位置当前竞价为
P={p1,p2,p3…pn}。对于任意的广告位i上获得位置的广告j有
(vj-pi)xi>=(Vj-Pi-1)Xi-1
则称，当前状况为均衡报价。需要注意的是，广义二阶价格的均衡点不唯一。并且，广义二阶价格不是一个激励相容的机制。广告主如果按照真实点击价值报价，并不一定是最优的选择。例如：
广告位和点击率
广告和点击价值
按照上表，此时如果按照真实点击价值报价为（5，2，1），而如果A降低报价为1.5，他将获得更大的利益。因此，广义二阶价格不是一个激励相容的机制。
尽管如此，由于广义二阶价格简单易行。当前国内各大互联网广告公司如百度、淘宝等，使用的关键词竞拍模式都是基于广义二阶价格拍卖。在真实的系统中，不会将广告简单的按照竞价扣费，扣费也不是简单的按照下家加一的方式进行。因为在CPC的广告场景下，需要考虑广告的点击率因素，即使是竞价很高的广告，如果点击率很低也不会给广告系统带来多大的收益，因此不应该给这类广告分配展现。因此，对于每条广告i，广告系统会首先预估广告i在当前展现场景下的点击率[图片]，结合其竞价[图片]，然后计算其每千次展现的期望收益为
ecpmi＝aibi＊1000
（原则上，[图片]，但是不乘常数项1000不影响后面的计算，所以就简化为
ecpmi＝aibi），然后将广告集合按照ecpm排序，选取排序靠前的若干条广告用于展现。在计费时，如果第i个广告被点击了，那么从广告主处扣除的费用为：
ai＋1bi＋1/ai＋最小的货币单位
这里i+1表示排名在i后面一位的广告。上式可见，广告的点击率越高，那么当它被点击事，从广告主处扣除的费用就越少。而广告平台采取这种方式扣费，可以激励用户优化广告质量提高广告点击率，从而也提高了整个广告系统的用户体验。
而淘系里面不仅仅是点击率，而是质量得分代表着这个词是否匹配这个广告
于是就有了
你的扣费＝下一名的质量得分＊下一名的出价／你的质量得分＋0.01
松子电商运营日记
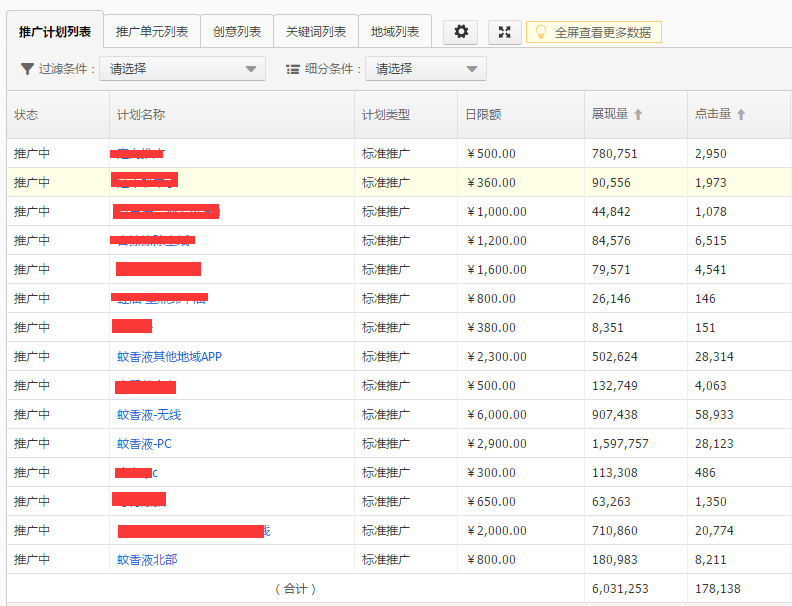
羽绒服类目飙升榜单
2015年双十一热词
